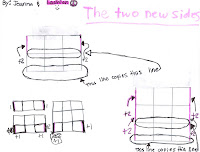
The first rectangle has a perimeter of 8, the second 10, and the third 12. Can you predict the perimeter of the fourth rectangle? The fifth? You probably can. It increases by 2" each time you add a row. Our first job was to figure out why. This student work explains why the perimeter increases by two each time you add a new row:
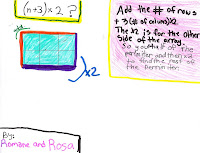
Next, we wanted to find out if we could find the perimeter of any number of rows without finding all the perimeters before it. We wanted to find the perimeter of a rectangle with 100 rows without knowing the 99th. We came up with these algebraic expressions for finding the perimeter for any number of rows (where n is the number of rows and the length equals three):
(n + 3) x 2
(n-1) x 2 + 8
2n + 6
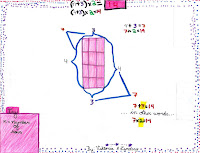
Once we knew that these expressions worked, we tried to find out why they work. Here's what we discovered:
(n + 3) x 2
(n-1) x 2 + 8
2n + 6
A note to grownups: The first algebraic expression, (n + 3) x 2 is a formula for perimeter. n is the number or rows, or the width, and 3, in this example, is the length. (length + width) x 2 = perimeter. Our purpose here wasn't to find a formula for calculating perimeter (which most students know how to do), it was to write equations that fit this situation and then figure out why they work.
Thanks for reading.